Research
"You see things; and you say, 'Why?' But I dream things that never were; and I say, 'Why not?'"
–– George Bernard Shaw (1856 –1950)
Our research spans different disciplines ranging from digital circuit design, to algorithms, to mathematics, to synthetic biology. It tends to be inductive (as opposed to deductive) and conceptual (as opposed to applied). A recurring theme is building systems that compute in novel or unexpected ways with new and emerging technologies. Often, the task of analyzing the way things work in a new technology is straightforward; however the task of synthesizing new computational constructs is more challenging – and more interesting!
Please see our Publications page for a full list of our papers. Here we highlight some of our research– some it recent, some of it not.
Storing Data with Molecules
All new ideas pass through three stages:
- It can't be done.
- It probably can be done, but it's not worth doing.
- I knew it was a good idea all along!
––Arthur C. Clarke (1917–2008)
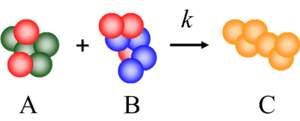
Ever since Watson and Crick first described the molecular structure of DNA, its information-bearing potential has been apparent to computer scientists. With each nucleotide in the sequence drawn from the four-valued alphabet of {A, T , C, G}, a molecule of DNA with n nucleotides stores 2n bits of data. Indeed, this information storage underpins life as we know it: all the instructions on how to build and operate a life form are stored in its DNA, honed over eons of evolutionary time.
Could humans store data in DNA? "Can't be done – too hard."
Is it worth doing? "Definitely not. It will never work as well as our hard drives do."
But one can store so much data so efficiently! "I knew it was a good idea all along!"
|

|

|
Computing with Molecules
“If I can’t create it, I don’t understand it.” –– Richard Feynman (1918–1988)
Computing has escaped – from desktops and data centers into the wild. Embedded microchips – found in our gadgets, our tools, our buildings, our soils, and even our bodies – are transforming our lives. And yet, there are limits to where silicon can go and where it can compute effectively. It is a foreign object that requires a power source (a battery or an AC plug). We are studying novel types of computing systems that are not foreign, but rather an integral part of their physical and chemical environment: systems that compute directly with molecules. A simple but radical idea: compute with acids and bases. An acidic solution corresponds to a "1", while a basic solution to "0":
|
It's more complex that acids and bases, but DNA is a terrific chassis for computing. We have developed "CS 101" algorithms with DNA: Sorting, Shifting and Searching:
|
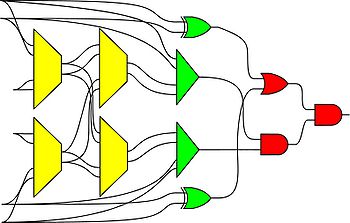
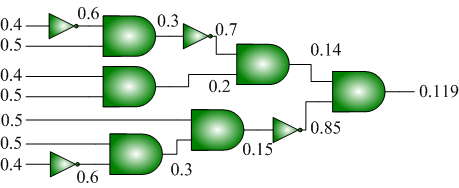
Just as electronic systems implement computation in terms of voltage (energy per unit charge), molecular systems compute in terms of chemical concentrations (molecules per unit volume). We have developed digital logic that operates on molecules:
|
|
 We map abstract molecular reactions to DNA reactions. Through a process called DNA strand displacement, single strands of DNA displace parts of double strands, releasing other single strands. |
Computational Constructs
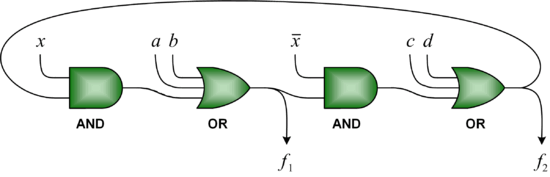
Based on a bistable mechanism for representing bits, we implement a constituent set of logical components, including combinational components such as AND, OR, and XOR gates, as well as sequential components such as D latches and D flip-flops. Using these components, we build full-fledged digital circuits such as a binary counters and linear feedback shift registers.
|
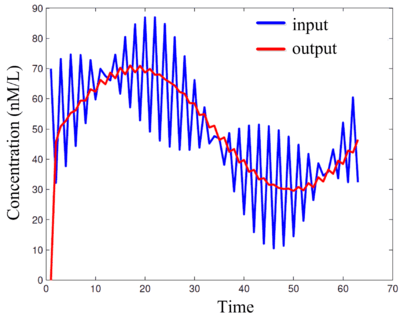
We have developed a strategy for implementing signal processing with molecular reactions including operations such as filtering. We have demonstrated robust designs for Finite-Impulse Response (FIR), Infinite-Impulse Response (IIR) filters, and Fast Fourier Transforms (FFTs).
|
|
|
Please see our "Publications" page for more of our papers on these topics.
Computational Immunology
“Biology is the study of the complex things in the Universe. Physics is the study of the simple ones.” –– Richard Dawkins (1941– )
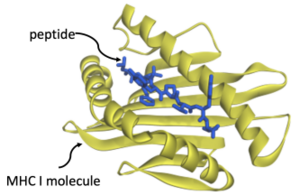
We are studying a problem that computer science currently judges to be very difficult: to predict cellular immunity. It centers on the question of how strongly a given molecule binds to another. The given molecule is a peptide – a fragment of a protein derived from a pathogen, such as a virus. The other is a molecule called Major Histocompatibility Class I (MHC I) that is expressed on the surface of most of our cells. MHC I molecules have a cleft into which a peptide can bind. A peptide will only bind if it fits into the cleft like a key into a lock.
The binding is a critical step in a critical component of the immune system: it allows circulating T-cells to kill off infected cells. If this mechanism succeeds, an infection is stopped in its tracks. If it fails, then infected cells become factories for reproducing copies of the virus and full-blown disease results. Most aspects of the chemistry are well understood. The difficulty lies with the combinatorial scale . There are 38,000 peptides for a virus like SARS- Cov-2 each paired with 21,000 variants of MHC I molecules in the human population. This translates to three-quarters of a billion distinct pairings. Simulating them all would take billions of days, of computing time – clearly an intractable proposition. But we are turning billions of days of computing time into just a few weeks of cloud computing time, donated by Oracle:
|
The first step is to solve the problem of hydrophobicity:
|
The next is to understand the role of variants:
Computing with Random Bit Streams
"To invent, all you need is a pile of junk and a good imagination." –– Thomas A. Edison (1847–1931)
Humans are accustomed to counting in a positional number system – decimal radix. Nearly all computer systems operate on another positional number system – binary radix. From the standpoint of representation, such positional systems are compact: given a radix b, one can represent bn distinct numbers with n digits. However, from the standpoint of computation, positional systems impose a burden: for each operation such as addition or multiplication, the signal must be "decoded", with each digit weighted according to its position. The result must be "encoded" back in positional form. Any student who has designed a binary multiplier in a course on logic design can appreciate all the complexity that goes into wiring up such an operation.
Logic that Operates on Probabilities
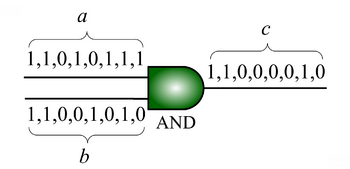
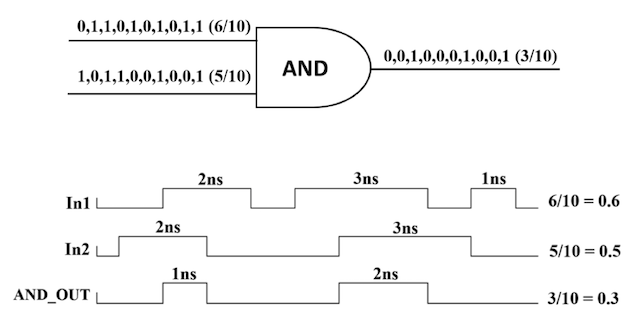
We advocate an alternative representation: random bit streams where the signal value is encoded by the probability of obtaining a one versus a zero. This representation is much less compact than binary radix. However, complex operations can be performed with very simple logic. For instance, multiplication can be performed with a single AND gate; scaled addition can be performed with a multiplexer (MUX).
We have developed a general method for synthesizing digital circuitry that computes on such stochastic bit streams.
|
|
Logic that Generates Probabilities
Schemes for probabilistic computation can exploit physical sources to generate random values in the form of bit streams. Generally, each source has a fixed bias and so provides bits that have a specific probability of being one versus zero. If many different probability values are required, it can be difficult or expensive to generate all of these directly from physical sources. In this work, we demonstrate novel techniques for synthesizing combinational logic that transforms a set of source probabilities into different target probabilities.
|
Computing with Crappy Clocks
Clock distribution networks are a significant source of power consumption and a major design bottleneck for high-performance circuits. We have proposed a radically new approach: splitting clock domains at a very fine level, with domains consisting of only a handful of gates each. These domains are synchrnonized by "crappy clocks", generated locally with inverter rings. This is feasible if one adopts the paradigm of computing on randomized bit streams.
|
Please see our "Publications" page for more of our papers on these topics.
Computing with Feedback
"A person with a new idea is a crank until the idea succeeds." –– Mark Twain (1835–1910)
The accepted wisdom is that combinational circuits (i.e., memoryless circuits) must have acyclic (i.e., loop-free or feed-forward) topologies. And yet simple examples suggest that this need not be so. We advocate the design of cyclic combinational circuits (i.e., circuits with loops or feedback paths). We have proposed a methodology for synthesizing such circuits and demonstrated that it produces significant improvements in area and in delay.
|
Please see our Publications page for more of our papers on this topic.
Computing with Nanoscale Lattices
"Listen to the technology; find out what it’s telling you.” –– Carver Mead (1934– )
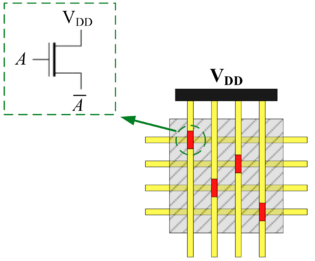
In his seminal Master's Thesis, Claude Shannon made the connection between Boolean algebra and switching circuits. He considered two-terminal switches corresponding to electromagnetic relays. A Boolean function can be implemented in terms of connectivity across a network of switches, often arranged in a series/parallel configuration. We have developed a method for synthesizing Boolean functions with networks of four-terminal switches. Our model is applicable for variety of nanoscale technologies, such as nanowire crossbar arrays, as molecular switch-based structures.
|
The impetus for nanowire-based technology is the potential density, scalability and manufacturability. Many other novel and emerging technologies fit the general model of four-terminal switches. For instance, researchers are investigating spin waves. A common feature of many emerging technologies for switching networks is that they exhibit high defect rates.
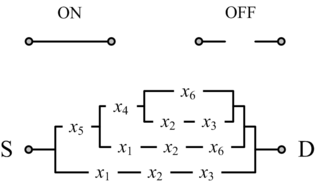
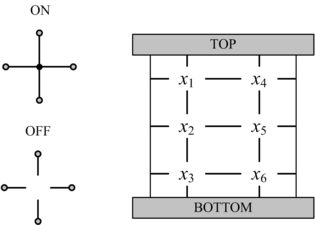
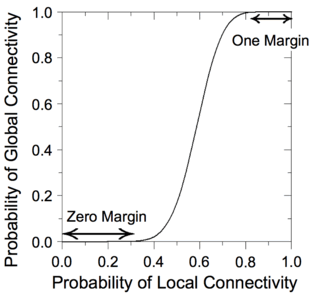 In a switching network with defects, percolation can be exploited to produce robust Boolean functionality. Unless the defect rate exceeds an error margin, with high probability no connection forms between the top and bottom plates for logical zero ("OFF"); with high probability, a connection forms for logical one ("ON"). |
We have devised a novel framework for digital computation with lattices of nanoscale switches with high defect rates, based on the mathematical phenomenon of percolation. With random connectivity, percolation gives rise to a sharp non-linearity in the probability of global connectivity as a function of the probability of local connectivity. We exploit this phenomenon to compute Boolean functions robustly in the presence of defects.
|
Please see our "Publications" page for more of our papers on these topics.
Algorithms and Data Structures
"There are two kinds of people in the world: those who divide the world into two kinds of people, and those who don't." –– Robert Charles Benchley (1889–1945)
Consider the task of designing a digital circuit with 256 inputs. From a mathematical standpoint, such a circuit performs mappings from a space of Boolean input values to Boolean output values. (The number of rows in a truth table for such a function is approximately equal to the number of atoms in the universe – rows versus atoms!) Verifying such a function, let alone designing the corresponding circuit, would seem to be an intractable problem. Circuit designers have succeeded in their endeavor largely as a result of innovations in the data structures and algorithms used to represent and manipulate Boolean functions. We have developed novel, efficient techniques for synthesizing functional dependencies based on so-called SAT-solving algorithms. We use Craig Interpolation to generate circuits from the corresponding Boolean functions.
|
Please see our "Publications" page for more of our papers on this topic. (Papers on SAT-based circuit verification, that is, not on squids.)
Mathematics
"Mathematics may be defined as the subject in which we never know what we are talking about, nor whether what we are saying is true." –– Bertrand Russell (1872–1970)

The great mathematician John von Neumann articulated the view that research should never meander too far down theoretical paths; it should always be guided by potential applications. This view was not based on concerns about the relevance of his profession; rather, in his judgment, real-world applications give rise to the most interesting problems for mathematicians to tackle. At their core, most of our research contributions are mathematical contributions. The tools of our trade are discrete math, including combinatorics and probability theory.

|
Please see our "Publications" page for more of our papers on this topic.
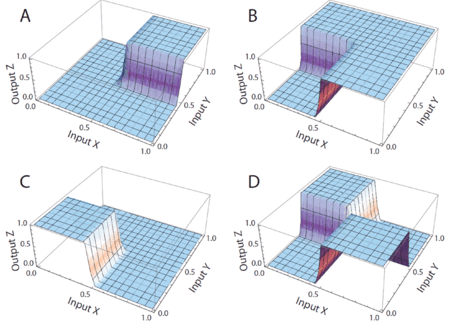
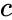 that is the product of the of the input probabilities
that is the product of the of the input probabilities  and
and 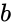 .
.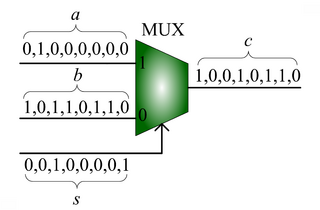
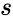 , the MUX produces an output probability
, the MUX produces an output probability 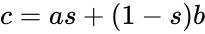 .
.
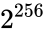 Boolean input values to Boolean output values. (The number of rows in a
Boolean input values to Boolean output values. (The number of rows in a 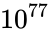 rows versus
rows versus 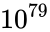 atoms!) Verifying such a function, let alone designing the corresponding circuit, would seem to be an intractable problem. Circuit designers have succeeded in their endeavor largely as a result of innovations in the data structures and algorithms used to represent and manipulate
atoms!) Verifying such a function, let alone designing the corresponding circuit, would seem to be an intractable problem. Circuit designers have succeeded in their endeavor largely as a result of innovations in the data structures and algorithms used to represent and manipulate